Montmort’s Theorem: Statistisk stoleleg
For nogen tid siden faldt jeg over denne side, der stiller følgende drilleopgave: (Lad være med at trykke på linket, hvis du selv vil pusle med den)
Hvis nu n studerende, der sidder på n forskellige pladser i et lokale alle sammen rejser sig op (fx for at holde pause, hente kaffe eller hvad de nu gør, sådanne væsener) og når de så kommer tilbage i lokalet sætter sig på en helt tilfældig plads.
Hvad er så sandsynligheden for at mindst én person sidder på sin oprindelige plads? Hvad sker der med sandsynligheden efterhånden som n stiger?
Intuitivt virker det som om det skal blive meget mindre sandsynligt, efterhånden som n stiger.
Det er jo ret hurtigt at se at hvis n=1, så er sandsynligheden 100% - der er kun den samme person, og den samme plads. Hvis n=2, så sidder de enten begge på deres pladser eller ingen af dem gør. nu er sandsynligheden altså kun 50%. For n=3 sker der dog allerede noget sjovt… sandsynligheden stiger pludselig til 66.7% (2/3), da kun 2 ud af 6 mulige kombinationer af bagdele og stolesæder medfører at alle får nye pladser.
Hmmm… Der må være noget los… Men hvad?
Lad os alle regne!
Finten er i kravet “mindst én skal have sin oprindelige plads” — havde det været “kun én” eller “ingen”, så havde det været væsentlig lettere at regne på, men som det står nu, så skal der gribes dybt i kassen med matematik. Altså den rigtige slags, med bogstaver. Ikke bare almindelig regning. Det er jeg jo ikke meget for1, så jeg valgte snydeløsningen og simulerede det i stedet.
Det bliver jo hurtigt dyrt i kaffe, hvis man skal have n studerende til at vade rundt på gangene en million gange, så jeg greb fat i noget R-kode. Ikke verdens hurtigste løsning, men i det mindste kunne den køre mens jeg sov.
Jeg tog altså og lod antallet af studerende, n, variere fra 1 til 50, og for hvert antal lod jeg dem holde pause 10.000.000 gange. Dette er (også) et eksempel på Monte Carlo simulering som jeg har skrevet om før
Herefter undersøgte jeg hvor stor en andel af de forskellige kørsler der resulterede i at mindst én studerende ramte sin egen plads.
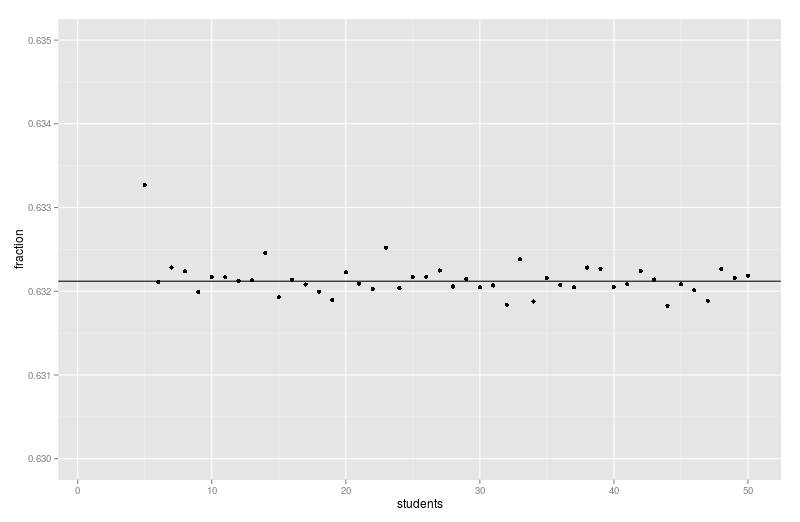
Det kom til at se således ud:
Jeg har zoomet ret kraftigt på y-aksen, så de første 4 punkter ligger udenfor grafen, men da jeg har opskrevet de første tre ovenfor, så går det nok.
Det vi ser her er et typisk resultat fra en Monte Carlo simulering der konvergerer mod en bestemt værdi, men alligevel hopper lidt rundt om den, fordi usikkerheden på de sølle 10 millioner kørsler er større end forskellen fra målværdien.2.
Det viser sig ud fra ovenstående at lige så snart \(n \approx 6\), så udvikler den sig ikke længere, men stort set er lig med den spøjse konstant \(\frac{1}{e}\).
For at se hvordan det kan være er det desværre ikke nok at løse den
numerisk/simuleret — her er man nødt til at være analytisk, men da det
involverer fæle begreber som
derangements, og kræver at
man kan folde en rekursiv formel om til en
sommerhat rækkeudvilking/sumform, så vil jeg lade den ligge indtil
jeg finder et større stykke papir — og/eller en venlig l[æø]ser
sender den til mig.3
Jeg synes bare at resultatet var så sjovt at jeg måtte a) teste og b) dele det.
Så der har vi det altså — i både en lille forsamling, en gennemsnitsklasse og et helt førsteårshold er der ca. 63.2% chance for at mindst én studerende sidder på sin egen plads igen, hvis de alle rejser sig og fordeler sig tilfældigt.
\Worm — der føler sig lidt permuteret.
-
I hvert fald ikke når den skal være stringent. Kombinatorik er åbenbart svært! 4 ↩
-
Ja, man skal bruge RIGTIG MANGE kørsler, hvis man skal være meget præcis. ↩
-
Jeg tilbyder intet andet honoar end at blive udøddeliggjort i disse annaler. ↩
-
Anekdotisk i hvert fald svært inden kaffe og tocifrede tidspunkter. ↩