Monte Carlo-simulationer: Med \(\pi\) på casino?
Okay… Måske er overskriften lidt misvisende — der er trods alt ikke mange nørder der dyrker hassardspil i stor stil, idet lotterier jo bare er en form for ekstraskat på folk der ikke kan regne.
Ikke desto mindre er der er disciplin eller metodik der netop kaldes Monte Carlo simulering fordi den netop forsøger at simulere eller modellere et systems opførsel gennem analyse af et stort antal tilfældige eksperimenter.
Det lyder lidt langhåret, og er det egentlig også i sin rene, teoretiske form, men princippet er ret simpelt og det er ret smuk nørd når det virker og ret fascinerende at lege med.
Jeg kom i tanke om at Numberphile har en fin video om hvordan man kan estimere \(\pi\) med en æske tændstikker og de forklarer egentlig ideen ret godt.
Jeg overvejede at gøre det samme, eller måske skrive et program der kunne det, men så opdagede jeg at det var der nogen der allerede havde gjort. Nå, så må jeg jo gøre noget andet.
Nårh, ja… Man kan også bare bruge en dartskive og en tilstrækkeligt beruset værthusgæst. Det lyder mere som min slags simulering.
Lad os alle regne…
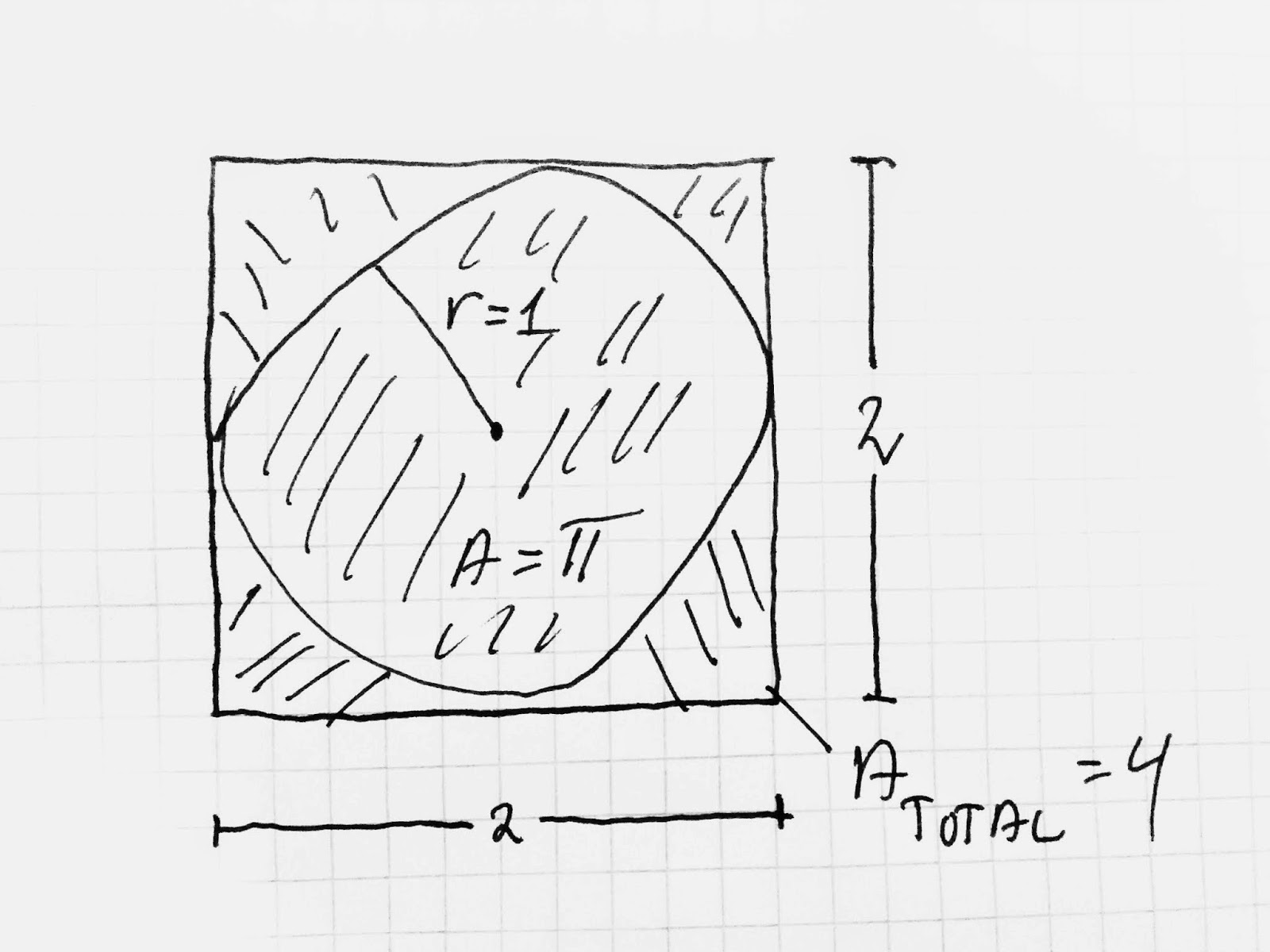
Vi ved jo alle at arealet af en cirkel (som fx en dartskive) er \(A=\pi \cdot r^2\), hvilket vil sige at har man en cirkel med radius 1, så har den arealet \(\pi\). Tegner man nu et kvadrat udenom, så har det arealet 4.
Begynder vi nu helt tilfældigt og uden at sigte1 at kaste dartpile imod kvadratet2, så vil \(\frac{\pi}{4}\) af de kastede dartpile ramme cirklen, og de resterende vil ramme kvadratet udenfor cirklen, da dette er forholdet mellem deres arealer. En skitse er vist på sin plads:
Hvis I nu bare ser bort fra at min cirkel er ret skæv og frihåndstegnet, så går det jo nok alt sammen. Nu skal vi altså bare drikke os godt stive og kaste dartpile hele natten, så kan vi estimere \(\pi\).
Jeg foreslår en fortløbende simulation i en eller flere af SDUs fredagsbarer med en vandrepokal, der uddeles ved slutningen af hvert semester til dem der er tættest på den sande værdi af \(\pi\).3
Hmmm…. det kan jo godt tage lidt tid at opnå en tilstrækkeligt god tilnærmelse4 — gad vide hvor mange dartpile man skal kaste før det er godt…
Jeg kunne jo spørge min trofaste ven R, der måske ikke er så specielt fordrukken5, men til gengæld kan kaste 100.000.000 virtuelle dartpile på ca. 30 sekunder6, og så se hvordan det konvergerer.
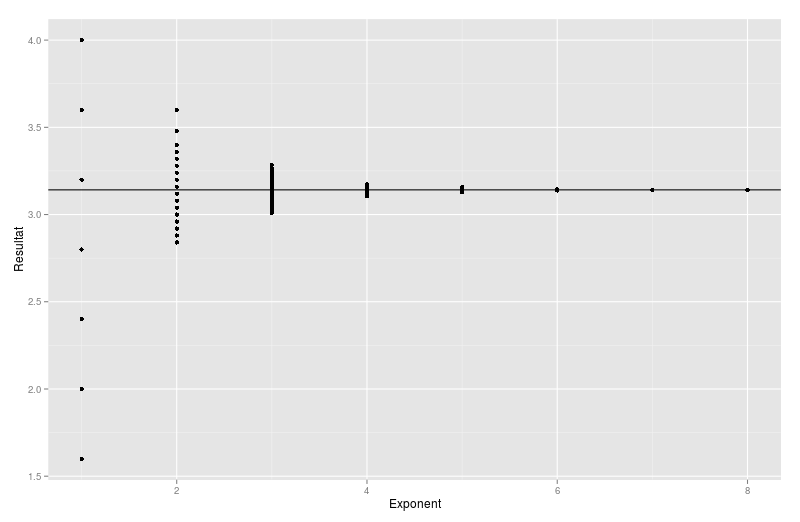
Jeg kastede altså lynhurtigt lige 20 linier kode sammen, der simulerede en kvart dartskive — resultatet er jo det samme, selvom man kun ser på første kvadrant og kastede fra 10 til \(10^8\) dartpile 100 gange hver, og plottede resultatet:
Det ses nu relativt tydeligt at med 10, 100 og 1000 dartpile er der stadig en hel del spredning på de 100 estimater, men lige så snart vi når op over \(10^6\) dartpile, så er spredningen faktisk ret lille.
Den relative standardafvigelse på resultatet falder fra ca 19% til ca. 48ppm når vi går fra 10 til \(10^8\) dartpile. 48 ppm svarer til en fejl på 48 mm per km, hvis det var et længdemål, så det er bestemt godt nok til rockmusik — og følgelig er standardfejlen på middelværdien endnu mindre.
Nå, men det var jo relativt tilforladeligt — og det er da fascinerende at man kan bestemme en naturkonstant så præcist ved at kaste dartpile helt tilfældigt!
Jaja — det kan godt være at man skal bruge rigtig mange dartpile hvis man skal ramme præcist nok til at bukke en partikelaccelerator — men jeg synes nu stadig det burde være en fredagsbarsdisciplin!
Hvis ikke det nok blev for farligt, så kunne man fristes til at lave det til en øvelse i \(\pi\)stolskydning…
Som altid udleveres kode og resultater ved henvendelse.
\Worm — der altid indrømmer hvornår han simulerer…
tilnærmelser i fredagsbaren, fra første til N’te orden.
-
Simuleres lettest ved indtag af tilstrækkelige mængder mørkt øl eller anden velbehagelig formulering af ethanol til human konsum. ↩
-
Og kun tælle dem der rent faktisk rammer selve kvadratet, inklusive cirklen indeni. Væggen må du spartle med tømmermænd i morgen.7 ↩
-
Det er trods alt dem der er mest berusede / tilfældige. Jeg stemmer på TEK, men nu er jeg jo også selv sådan en lidt af en ingeniørsut… ↩
-
Til \(\pi\), altså - der er sikkert masser af andre slags ↩
-
Ja, R er måske lidt sløvt for meget store N, selv fuldt vektoriseret, men hvis nogen vil tage udfordringen op i octave/MATLAB/Python/C/Haskell/??? - så kom bare an… ↩
-
Som en af mine gode venner udtrykte det så smukt en gang: “Nogen danser med ulve. Jeg saver med tømmermænd” ↩