Benfords lov
Indledning
Hvad har valgfusk, kreativ bogføring, fysiske konstanter og ugebladet Ingeniøren til fælles?
De er alle på et eller andet tidspunkt blevet undersøgt for overensstemmelse med Benfords lov.
Benfords lov, som er en observeret sammenhæng, snarere end en universel fysisk lovmæssighed, siger lidt forsimplet at hvis man tager en stor mængde tal fra virkelige kilder, så vil det første ciffer i tallet ikke være jævnt fordelt i intervallet 1 til 9. Faktisk vil det første ciffer være 1 ca 30% af gangene, 2 ca 18% af gangene, og de følgende tal vil optræde fortsat sjældnere.
Den eksakte sandsynlighed for at det første ciffer er d kan beregnes som følger: \(P(d)=log_{10}(1+ \frac{1}{d})\)
Det interessante er imidlertid ikke hvordan formlen ser ud, men hvorfor det forholder sig således, hvornår man kan regne med at det gælder, og hvad man kan bruge det til.
Hvorfor?
Hvorfor er det overhovedet interessant at beskæftige sig med hvilke cifre tal starter med, ud over som en øvelse i rekreativ matematik? Jo, fordi som jeg (og mange andre) tidligere har dokumenteret så er mennesker rigtigt dårlige til at generere “tilfældige” tal, så hvis man for eksempel fusker med regnskaber, valgresultater eller videnskabelige data, så er der en mulighed for at man kan opdage det ved at sammenligne data med Benfords lov. Dette er dog en omdiskuteret praksis, og mig bekendt har man ikke en international konsensus omkring hvornår et resultat er af en sådan statisktisk styrke at det kan bruges som “bevis”.
Hvornår?
Den bedste tilnærmelse til hvilke data Benfords lov gælder for er, at den gælder for alle udfald at virkelige processer, hvis resultater spænder over flere størrelsesordener, og som ikke er underkastet fordelinger der begræsner udfaldsrummet.
Det er jo lidt af en mundfuld, men det betyder i praksis at tal med et stærkt begræset udfaldsrum, eller en underliggende struktur så som datoer, årstal, telefonnumre og menneskers højde ikke kan forventes at adlyde Benfords lov, hvis man betragter dem alene. Eksempelvis er der en forsvindende lille del af menneskers højder der starter med andet end 1, hvis man regner i meter.
Resultater fra sammensatte systemer eller datasæt, derimod vil ofte følge denne sammenhæng. Jeg vil forvente at eksempelvis indbyggertallet i danske kommuner vil være et godt datasæt at bruge som øvelse, hvis man vil lege med nogle tal selv. Arealer af lande, længder af floder og selv naturkonstanter har vist sig at følge sammenhængen.
Hvorledes?
Men hvorfor er det sådan? Det er et rigtig godt spørgsmål, og ikke trivielt at besvare — ja, faktisk er det ikke alle systemer hvor man i det hele taget har et godt svar på hvorfor det er sådan, men hvis man kigger på et fænomen som befolkningstal, så vokser sådan nogle oftest eksponentielt, dvs. med en bestemt procentsats hvert år, hvilket jo vil medføre at jo større tallet er, jo hurtigere vokser det.
Kvalitativt betragtet giver det således mening at tallet tilbringer længere tid med at starte med 1 - for så er det et relativt lille tal (uanset antallet af nuller der sættes efter), og derfor vokser det langsomt. Lige så snart tallet er vokset så meget at det starter med 2 vokser det også dobbelt så hurtigt og tilbringer derfor kortere tid med at starte med 2, og så fremdeles indtil tallet bruger meget kort tid med at starte med 9, inden det får et nul mere, og derpå atter starter med 1, og så begynder cyklussen forfra.
Tager man nu et stort antal befolkningstal, vil de således fordele sig som beskrevet ovenfor, idet de alle er et tilfældigt sted i cyklussen.
Læsere med hang til talskubberi vil nu have bemærket at dette jo netop stemmer fint overens med at der er en logaritme i fordelingsfunktionen, og faktisk var den første indikation af Benfords lov at en astronom opdagede tilbage i 1881 at hans bog med logaritmetabeller var mest slidt på de første sider - et godt eksempel på at en lille undren kan føre til ny viden.
Forsøg
Som et eksperiment tog jeg den nærmeste avis, i dette tilfælde Ingeniøren, nr. 26 fra 2013 og bladrede den igennem og skrev alle de tal der stod i den op, fraregnet sidetal, telefonnumre, datoer og år. Jeg så også kun på det redaktionelle indhold og annoncer deriblandt, og inkluderede ikke stillingsannoncerne. Derved fik jeg 138 tal, hvor det første ciffer fordelte sig som følger:
| Første Ciffer | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Antal | 48 | 25 | 16 | 16 | 9 | 11 | 7 | 2 | 4 |
Som det også ses af nedenstående plot, så er dette i god overensstemmelse med hvad man ville forvente, ifølge Benfords lov. Afvigelserne fra “det perfekte fit” er ikke større end det tilladelige, givet størrelsen af datasættet og en \(\chi^2\)-test viser da også at man ikke kan forkaste nulhypotesen om at tallene følger Benfords lov \((p=0.547)\).
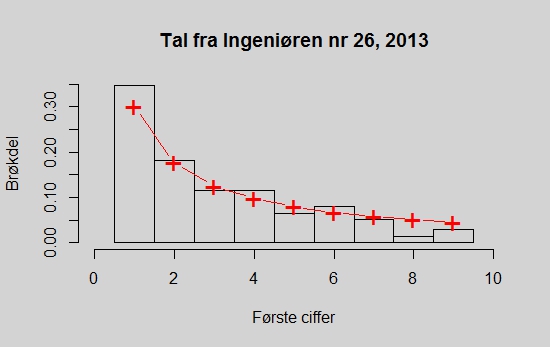
Observationer af første ciffer i tal fra Ingeniøren nr. 26, 2013 (søjler) og den teoretiske fordeling (+)
Outro
Benfords lov har mange andre sjove egenskaber — den er fx uafhængig af hvilke enheder man måler i, den har været brugt til mange forskellige slags undersøgelser, og selvom baggrunden for den kan virke noget kringlet, så dukker den op utroligt mange steder. Det er som minimum et godt stykke legetøj. :-)
Hvis du skulle have lyst til at læse mere, så kender jeg desværre ikke mange gode kilder på dansk, men jeg kan anbefale den engelske wikipedia, og Khan Academy har et par udmærkede videoer om emnet: Video 1, Video 2 og ellers er der jo altid Benfords oprindelige artikel.
\Worm