Dyre kort?
Tilsyneladende er den helt store dille1 blandt børn (og deres forældre) for tiden at samle dyrekort — hvilket, baseret på en forholdsvist lille stikprøve, i og for sig selv lader til at være en både hyggelig og lærerig oplevelse. Temaet er havdyr, og jeg forsøger at undgå dårlige (vandede?) vittigheder om “korthajer”…
Imidlertid er der, som altid, en vandslange i paradis, og i dette tilfælde hedder den “stikprøveudtagning” til mellemnavn2.
Der er adskillige forældre der er blevet godt gammeldags facebookfornærmede over hvor svært det er at få et fyldt samlehæfte, og det har været debatteret i radio, tv og online i rigt mål. Forbrugerombudsmanden har vist nok også fået en skrivelse.
Jeg vil slet ikke forholde mig til rimeligheden, men blot forsøge at se lidt på matematikken i det.
Lad os alle regne…
En lynhurtig øvelse i google-fu, og 5 minutter i selskab med Detektor fra DR2 fortæller mig at der i alt er fremstillet 87.290.351 “normale” kort, som der er 110 forskellige af og 5.819.357 “specialkort” som der er 30 forskellige af. Der er forestillet lige mange af hver af kortene i hver kategori.
Et af de fremførte klagepunkter er at det er for svært at få fat i specialkortene, men her har jeg en fornemmelse af at vi har fat i en form for bekræftelsesslagside i argumentet — jovist er de sjældnere, men faktisk ikke SÅ meget igen.
Laver vi divisionen kan vi hurtigt nå frem til at der er fremstillet ca 800.000 af hvert af de “normale” kort og ca. 190.000 af hvert af de “sjældne”. Så jo, de er sjældnere, men kun cirka en faktor 5, så inden vi overhovedet begynder at overveje dén faktor, så lad os se lidt på hvor svært det er bare at samle 140 forskellige kort med ens sjældenhed.
Vi skal trække kortene “op af en hat” — om vi gør det ét ad gangen eller 4 ad gangen er ikke specielt vigtigt for dette første overslag. Jeg tillader mig at regne med en uendelig pulje af kort, da ca. \(10^8\) kort er ret tæt på i praksis.
Vi forestiller os nu det scenarie at vi skal trække 140 forskellige kort ud af denne uendelige pulje i ét forsøg.
Det første kort vi trækker er ikke et vi har i forvejen, så sandsynligheden for at det er unikt er 140/140 = 1. Det næste er unikt i 139/140 tilfælde, det næste i 138/140 tilfælde etc. indtil vi rammer 1/140 for det sidste kort. Alle disse sandsynligheder skal vi gange med hinanden, da det er uafhængige forsøg — det næste kort vi trækker er ikke afhængigt af hvad vi allerede HAR trukket3.
Hele denne række bliver til \[P=\frac{140!}{140^{140}} = 4.7\cdot 10^{-60}\] Eller cirka 1 ud af 200.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.
Okay — så hvis der er 4 kort i en pakke så skal man nok ikke regne med at kunne nøjes med at købe nok ind til at skaffe 35 pakker…
Af ovenstående argument kan man også se, hvad alle samlere (af hvadsomhelst) allerede ved i praksis — jo større samling man allerede har, jo sværere er det at få fat i noget man ikke har, bare ved at trække tilfældigt — så skal man til at handle eller bytte… Men det er jo mere økonomi og psykologi end matematik, så det vil jeg overlade til nogen der har gået til det.
Men hvor mange kort skal man så have, før man har en nogenlunde rimelig chance for at kunne fylde samlehæftet?
Nu bliver matematikken en anelse mere langhåret, idet vi jo er ude i en situation hvor sandsynligheden for at få et nyt, ukendt kort bliver mindre og mindre, jo flere kort man allerede har — og da kombinatorik (som tidligere konstateret) er svært, så vælger jeg som sædvanligt at simulere mig ud af det. Det har også den fordel at jeg kan regne på sjældne kort også og stadig overstå det hele på under 20 linier kode og få et ret godt estimat med en køretid på ca 1 min.
Bemærk at der stadig er noget “jitter” — det burde være en glat kurve, men da jeg ikke helt har tålmodighed (eller togtur) nok til at lave mere en 1000 gentagelser på hvert punkt, så bliver det lidt støjende. Jeg er sikker på at I sagtens kan glatte kurven ud i hovedet, ellers må I komme forbi og låne et strygejern.
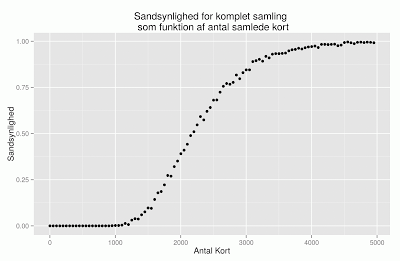
Herved fremkommer følgende:
Heraf ses det (ikke særligt overraskende) at sandsynligheden for at have en komplet samling først begynder at afvige væsentligt fra nul når man begynder at have anskaffet sig omkring 1000 kort, og rammer ca 50% omkring de 2200 kort.
Bemærk at ganske som forventet så bliver kurven fladere og fladere jo flere kort man får — og hvis det ser ud som om at det bliver 100% sikkert at få en fuld samling, hvis man har 5000 kort, så beklager jeg — den er i virkeligheden kun omkring 99.2%.
Kan man “nøjes” med ca 90% chance for et komplet sæt, så kan man ligeledes “nøjes” med cirka 3200 kort.
På DR har de haft en rigtig statistiker til at regne på det, og hun får nogle lidt andre tal, men det skyldes jo nok at hun regner eksakt og analytisk og med de præcise tal, hvorimod jeg bare sidder og sjusser mig igennem det som tidsfordriv på en lang togtur… Men helt skeløjet er det nu ikke, og det var fin underholdning.
Har du lyst til at supplere, kritisere, integrere, inspicere kode eller på anden måde interagere, så er alle kanaler som vanligt åbne.
\Worm
slå en 6’er (med en lige terning), selvom man lige har slået 4 i træk.