Ingeniørporno: Gættepinde og logaritmer
But what was happening now . . . this was magical. Ordinary men had dreamed it up and put it together, building towers on rafts in swamps and across the frozen spines of mountains. They’d cursed and, worse, used logarithms. They’d waded through rivers and dabbled in trigonometry. They hadn’t dreamed, in the way people usually used the word, but they’d imagined a different world, and bent metal around it. And out of all the sweat and swearing and mathematics had come this . . . thing, dropping words across the world as softly as starlight. — Terry Pratchett: Going Postal
Ja, jeg kunne ikke dy mig for at starte med et af mine yndlingscitater fra Discworldserien, dels fordi det berører dagens emne, men også fordi det meget godt viser ingeniør- og pionérånden og er ganske poetisk omkring hvordan man ændrer en verden med en god idé.
Men udgangspunktet for dette indlæg er såmænd noget så prosaisk som en bortkommet hæftemaskine.1 Det var nemlig mens jeg ledte ganske desparat efter den i mine skuffer at jeg (gen)fandt denne sjove lille dims, og tænkte at der var udgangspunkt for noget / en (teknologi)historie:
Hvis billedet er lidt utydeligt, så beklager jeg — det er tilsyneladende det bedste min mobil magter under forholdene — men lad os tage det stille og roligt og analysere dimsen.
Ved første øjekast ligner det jo mest en lettere personlighedsspaltet og temmelig pyntesyg lineal, og den tjener da også det simple afstandsmål og den rette linies tegning udmærket. Imidlertid er dens eksistensberettigelse noget mere langhåret og langt mere anvendeligt.
“Jamen, Worm! Hvad ER det? Og hvorfor er det interessant?” hører jeg jer
hvisle mellem sammenbidte tænder, og bare rolig - jeg skal nok komme til
Skagen sagen meget snart, men nu skal I jo lige have mulighed for at
udfolde de små grå på egen hånd først.
Okay. Tænkepausen er ovre. Hvis I stadig sidder og ligner spørgsmålstegn skal I ikke have det dårligt af den grund — men nu lader vi som om vi ikke ved noget, og skal være teknologiarkæologer.
Lad os se: Det må have en betydning at næsten alle skalaerne er forskellige, at hele midtersektionen kan forskydes, men at skalaerne er parvist de samme som på den faste del. Den der skydedims der ligger ovenpå er nok en hjælp til at aflæse noget præcist.
Hov? Midten kan bevæge sig? Og har de samme skalaer som de faste dele?
Ja:
Okay. Lad os så starte med at se på det øverste sæt skalaer på den faste og bevægelige del. (dem der starter med rødt 8 ude til venstre) Skalaerne er er som sagt ens, jeg har bare flyttet tungen (ja, det kalder man altså den bevægelige del) lidt.
Hmmm… 1-tallet (det øverste) på tungen står ud for 2-tallet på den faste skala, og ser man nu på hvordan de øvrige tal matcher op, så begynder det at lugte af at vi lige har foretaget en multiplikation… ud for 2 på tungen ligger 4, ud for 3 ligger 6, ud for 4 ligger 8 etc… Det er jo en to-tabel, og vi startede med at konstatere at 1-tallet på tungen står ud for 2-tallet på den faste skala… Hmmm…. lad os prøve noget andet… Så burde det altså give en 3-tabel at sætte 1 (igen det øverste) ud for 3?
Lad os se… ud for 2,3,4,5 på tungen har vi nu 6,9,12,15 - de sidste to godt nok kun ud fra en forudsætning om at 1-tallet der følger efter 9 i virkeligheden betyder 10, og det følgende 2-tal 20 etc., men det er vel en meget rimelig antagelse, hvis den får det til at passe så godt? Det er i hvert fald alle sammen fine multipla af 3.
Men det fortæller os jo faktisk noget. Vi startede med at konstatere at skalaerne ikke var linære, men nu ved vi jo faktisk hvad de er — vi har lige multipliceret to tal ved at lægge et par linære afstande sammen - forskydningen af tungen i forhold til den faste del.
Der findes nemlig en funktion der har den egenskab af den laver multiplikation om til addition - og det er såmænd den forholdsvist velkendte og ganske ydmyge logaritme, om hvilken det gælder: \[\log(ab)=\log(a)+\log(b)\] Så hvis vi ønsker at multiplicere de to tal a og b, så skal vi bare tage logaritmerne til tallene og så lægge dem sammen og så tage antilogaritmen til resultatet og så har vi produktet. Og alle disse operationer foregår helt automagisk på grund af den måde som skalaerne er indrettet! Det er da decideret pornoidt! — I hvert fald for en ingeniør2
Vi har altså at gøre med en analog lommeregner - også kaldet en regnestok! 3 Højden af nørdmode i 50’erne4, selvom den har været kendt siden 1600-tallet, og oprindelig blev udviklet af en engelsk matematiker og præst, der fik en lys idé efter at Napier havde opdaget/udviklet logaritmen og den var blevet videreudviklet af en waliser jeg ikke havde hørt om før jeg lavede lidt research5.
Så simpel multiplikation som jeg har brugt som eksempler er måske lidt overkill at anvende en dims til, men hvad nu hvis jeg gerne vil multiplicere 15366 med 17? Så er man naturligvis nødt til at lave lidt fingergymnastik, men det ser ca. sådan her ud:
Ja, jeg har zoomet lidt kraftigt, da jeg ikke kunne bruge løberen til at aflæse, fordi den så var i vejen på billedet, men jeg har efter bedste evne placeret tungens øverste 1-tal ud for 15.36, og ud for 1.7 på tungen kan vi så aflæse 26 — og efter at have genetableret det rigtige antal nuller (3 - jeg har divideret det ene tal med 100 og det andet med 10), så får vi altså 26000 — min stakmaskine siger at det rigtige svar er 26112, og vi har altså en fejl på under 0.5%, og det tog ca 10 sek inklusive foto — og man kan med lethed gøre det mere præcist med nogle ret simple og elegante greb, men det vil jeg lade være op til den ivrige l[æø]ser at gennemskue.
Okay, nu ved vi hvad formålet er, men hvad kan den så, ud over at multiplicere?
Når man kan multiplicere, så er det jo ret trivielt at gennemskue at man også kan dividere — man vender bare processen om, så det gider jeg faktisk ikke gennemgå.
Derimod er der noget speget ved at der er to forskellige skalaer på både tungen og den faste del — men efter lidt meditation7 over det, vil jeg påstå at det er nærliggende at konkludere at det er fordi den øverste er kvadratet af den nederste!
Så nu kan vi altså også opløfte til anden potens — og uddrage kvadratrødder! Vi kan endda gøre det inde midt i et regnestykke ved at skifte mellem hvilken skala vi betragter som den aktive…
Der hvor det bliver rigtig sjovt er når man når til det faktum at hvis bare man har den rigtige skala, så kan man regne næsten hvad som helst ud!
Bevares — det kræver lidt fingergymnastik og af og til også at man kender til de der regneregler man lærte i gymnasiet og straks glemte fordi man ikke kunne se hvad formålet var…
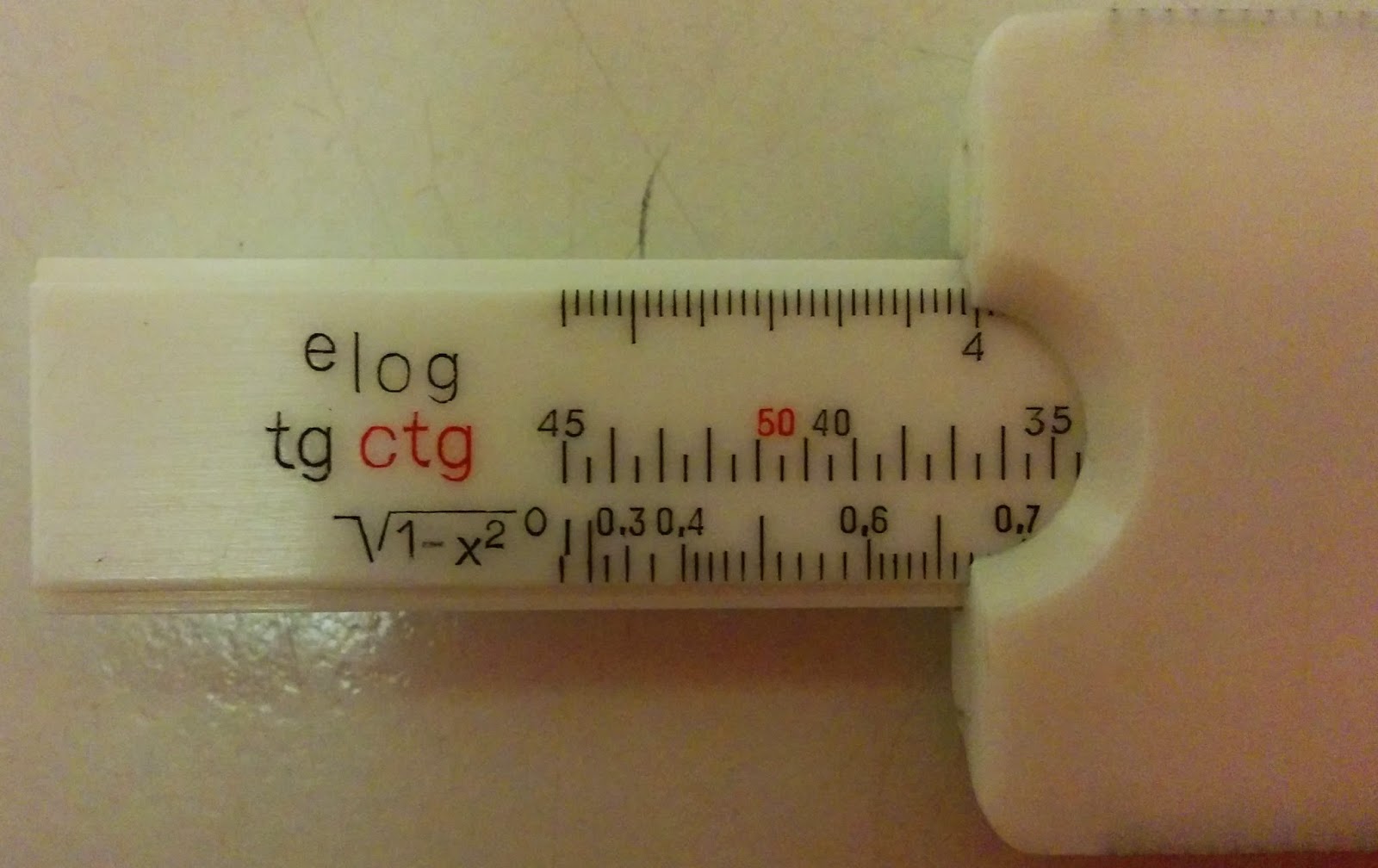
Bare på den lille og relativt basale regnestok8 jeg har leget med her er der således mulighed for, ud over multiplikation og division, at udregne sinus, cosinus, kvadratrødder, kubikrødder, opløfte til anden og tredje potens, uddrage logaritmer (sjovt nok den eneste helt linære skala) og hvis man enten vender tungen om eller bruger de snedige aflæsningsstreger der er angivet på bagsiden, så kan man også få logaritmer og antilogaritmer9 med grundtallet e i stedet for 10, beregne tangens og cotangens samt beregne værdien af \(\sqrt{1-x^2}\), som selv jeg har lidt svært ved at gennemskue hvorfor er smart, men lur mig om ikke den kan bruges til at tilnærme et eller andet… Måske noget trigonometri? Det ligner en størrelse der godt kunne have sådan en anvendelse, men jeg har ofte taget fejl.
Et lille kig på bagsiden med tungen trukket ud, så man kan se aflæseaggregatet til højre:
Bemærk firmamærket — tilsyneladende lavede LM Ericsson lommeregnere før de lavede mobiltelefoner :-)
Og den anden ende af tungen, med markeringer af skalaer:
Det var vist hvad jeg havde at sige om den sag, lige indledningsvis, men nu mener jeg også at have præsenteret dimsen nok til et førstehåndsindtryk.
Jeg håber I nød et lille stykke med historie og teknologiarkæologi. Hvis der (mod forventning?) skulle være interesse, så vil jeg da gerne se om jeg kan finde min (fars) gamle matematikståbi og lave en lille supplerende tutorial eller en lille video.
Indtil da, så bor min gættepind i min rygsæk eller skrivebordskuffe, hvorfra den rutinemæssigt vil blive hevet frem, når en kollega eller mednørd spørger om jeg har en lommeregner hun kan låne… Eller bare som backup i tilfælde af strømsvigt :-)
\Worm — der nu også kan nørde analogt
-
Den blev fundet igen. Den havde bare forklædt sig som bogstøtte i min reol. ↩
-
Det virker også af og til på matematikere, når bare lige de får forklaret hvorfor det er frækt… Men til deres forsvar skal det jo også siges at det er ret sjældent de rent faktisk skal regne noget ud numerisk. ↩
-
Let drillende ofte kaldet en gættepind - deraf overskriften - da den jo måske nok mangler absolut præcision, men er suveræn til hurtige overslag. ↩
-
Altså… 1950’erne. Så er jeg altså heller ikke ældre… ↩
-
Han var tilsyneladende også præst - men på den anden side, hvis man skal leve i cølibat, så må man jo have andre måder at finde tilfredsstillelse på10 ↩
-
Jerns smeltepunkt og året for reformationen. ↩
-
Det er en god indikation at 2 står over 1.4, 3 over 1.73, og 4 over 211 ↩
-
Fra min farfars tid i telegrafregimentet, Aaaaaarhus. Der er derudover et par store / lækre eksemplarer i familiens eje. Det er bare kun denne jeg nænner at have med i felten. ↩
-
En “antilogaritme” er bare en potensopløftning af grundtallet til operanden - hvis vi har en 10-tals logaritme er antilog10(2.5) altså \(10^{2.5}\) og hvis det er en naturlig logaritme er antiloge(2.5) altså \(e^{2.5}\). ↩
-
Glæden ved videnskabeligt gennembrud er måske knap så stor som den ved sex, men den varer til gengæld længere. Den kan dog være svært at opnå bare tilnærmelsesvis regelmæssigt. ↩
-
Ja, \(\sqrt{2}\) og \(\sqrt{3}\) optræder så ofte ude i virkeligheden at dem har de fleste ingeniører fået ind med — om ikke modermælken, så farvandet og fredagspilsneren. Man kan også rende længere op af skalaen, hvis man bedre kan lide heltal… ↩