01 DEC: Juletræer og fraktaler
De fleste har nok mødt en fraktal på et tidspunkt, eller som minimum set én i fangenskab. Den mest kendte er jo nok Mandelbrot-sættet, der ofte fremstilles grafisk på denne måde:
 Kilde: http://commons.wikimedia.org/wiki/File:Mandel_zoom_00_mandelbrot_set.jpg
Kilde: http://commons.wikimedia.org/wiki/File:Mandel_zoom_00_mandelbrot_set.jpg
Det der kendetegner fraktaler er at de bliver ved med at se ens ud, eller i det mindste har let genkendelige features, der går igen, uanset hvor meget man zoomer ind på dem. Hvis man zoomede ind på ovenstående billede indtil den lille sorte gnalling ude til venstre fyldte det hele, ville den være magen til billedet som det ser ud nu. Meget fascinerende, og du kan fx lege med det her.
Jeg vil ikke begynde at grave mig ned i matematikken, men den er ret sjov, forbløffende enkel, resultatet taget i betragtning, og hvis du vil vide mere om hvad der ligger bag kan du fx se det her.
I stedet vil jeg stille det lidt mærkelige spørgsmål: “Hvor mange
dimensioner har et juletræ?”
De fleste vil jo nok mene at det er
relativt let at afgøre at sådan en gevækst er tredimensionel (ellers var
den jo også lidt svær at danse rundt om og lægge pakker under). Men det
viser sig at det er her fraktalerne kommer ind i billedet. Et juletræ er
jo svagt fraktalt i sin struktur: En given sidegren, betragtet for sig
selv, er jo en udmærket (om end lidt mindre) tilnærmelse til et juletræ
i sig selv, og sådan kan man jo egentlig blive ved, indtil man står med
en håndfuld grannåle og et stort forstørrelsesglas. Du kan med fordel
lave det eksperimentelle arbejde på et bundt pyntegrønt — det skal
alligevel skilles ad.
Men hvad er det nu med fraktale dimensioner? Jo, det bedste eksempel er jo nok det klassiske:
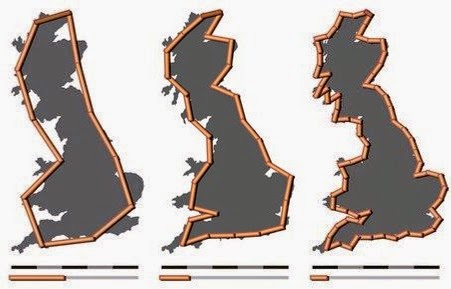
Hvis man forsøger at måle længden af et lands kystlinie, så ændrer resultatet sig, afhængigt af hvor lang din tommestok er!
Herover er et billede jeg har hugget fra http://commons.wikimedia.org/wiki/File:Britain-fractal-coastline-combined.jpg hvor det ses at hvis man bruger målestokke på hhv 200, 100 og 50 km, så bliver længden af den britiske kystlinie hhv. ca. 2350 km, 2775 km and 3425 km.
“Ægte” (matematiske) fraktaler er endnu værre til at opføre sig på denne måde, og derfor har man været nødt til at bøje det sædvanlige dimensionsbegreb en anelse.
Lidt populariseret er den fraktale dimension af et objekt et mål for hvor meget ekstra information man får, når man gør sin målestok mindre.
Den britiske kystlinie ovenfor er jo principielt en linie, og bør derfor have dimensionen én — men fordi der kommer mere information (længde) når man gør målestokken mindre, så nærmer den sig at opføre sig som en flade i stedet, men den kommer ikke hele vejen — vi får ikke 4 gange så meget kystlinie af at halvere målestokken, som hvis det var en flade.
Derfor kan man regne ud at dimensionen bliver 1.25. Ja, det er faktisk muligt at have dimensioner der ikke er hele tal, når man ser på det på denne måde. Det giver muligvis ikke så meget fysisk mening, men det er et mål for hvor “kringlet” noget er.
Kanten på mandelbrotfraktalen som jeg startede med har en dimension på
- Det vil sige at den linie der beskriver kanten, faktisk er så “uendelig” snørklet at den opfører sig som en flade, snarere end en linie.
På samme måde vil omkredsen af juletræet også være stærkt forskellig, afhængig af om man måler den i den traditionelle enhed “familiemedlemmer med udstrakte arme”, eller om man finder mikrometerskruen frem og går en tur på overfladen af nålene. Jeg vil overlade udregningerne til den ivrige l[æø]ser, der mangler noget at sidde og filosofere over, mens kaffen løber igennem og julelysene tændes…
\Worm — fraktalnisse (D~2.79)