Look-and-say sekvensen
Der er et hyggeligt gammelt hovedbrud der går på at fortsætte sekvensen:
1
11
21
1211
111221
312211
???
Og hvis man som de fleste andre hovedbrudsglade nørder læser det som heltal eller resultater af en funktion eller iteration over tallene, så får man i den grad hovedpine - der er tilsyneladende intet system overhovedet.
Nu vil jeg med det samme ødelægge det for mine læsere og forklare hvad finten er, så vi a) kan komme i gang med at lege med tal og b) I allerede har fået svaret og kan drille jeres lillesøster selvom I ikke orker at læse videre.
For at gennemskue den skal man betragte tallene som en mærkelig hybrid mellem en tekststreng og et tal — man skal simpelhen læse hver række, og lade den næste beskrive den.
Den første række er ét ettal. Derfor bliver den næste række 1-1. Dette er så to éttaller, og tredje række bliver 2-1. Når man læser denne højt er det ét total og ét ettal, og derfor får vi 1-2-1-1… og så videre, og så videre… Det er derfor den også kaldes “look-and-say sekvensen”.
Men hæng nu lidt på alligevel — denne talrække har nemlig adskillige sjove egenskaber.
Hvis man starter den med 1 (eller 2 eller 3), så optræder der på intet tidspunkt noget ciffer højere end 3, uanset hvor længe man itererer.
Jeg mindes engang i min grønne ungdom1 at have forsøgt at fortsætte den så langt jeg nu magtede, og det viser sig faktisk er være meget kort, ikke så meget fordi jeg er doven2, men fordi rækkens længde eksploderer meget hurtigt!
De første 10 trin går meget godt — længderne vokser stille og roligt men ikke uoverskueligt: 1, 2, 2, 4, 6, 6, 8, 10, 14, 20. Men allerede ved trin 16 er den over 100 cifre lang, og ved 25 krydser den de 1000 cifre, så det er ikke sådan lige til at arbejde med i hånden.
Men heldigvis har vi jo computere, så en time og lidt python-fu senere, så kan man med lethed både generere talrækkerne og tabeller over deres længder.3
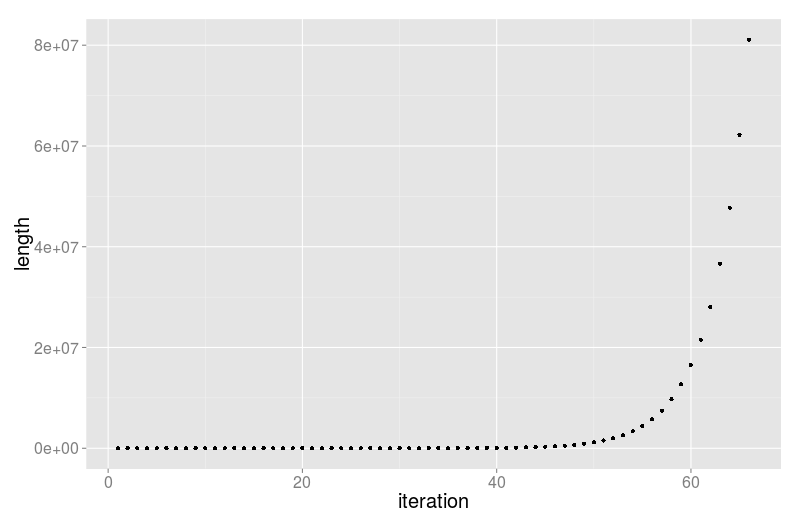
Det giver ikke helt vildt meget mening bare at liste nogle enorme talstrænge op eller tabulere deres længder, så jeg har lavet et lille plot (klik for at forstørre):
Vi kan nu se at længden stiger jævnt, men ikke lineært og at når vi når op omkring de 60 iterationer, så er vi oppe i størrelsesordenen millioner af cifre.
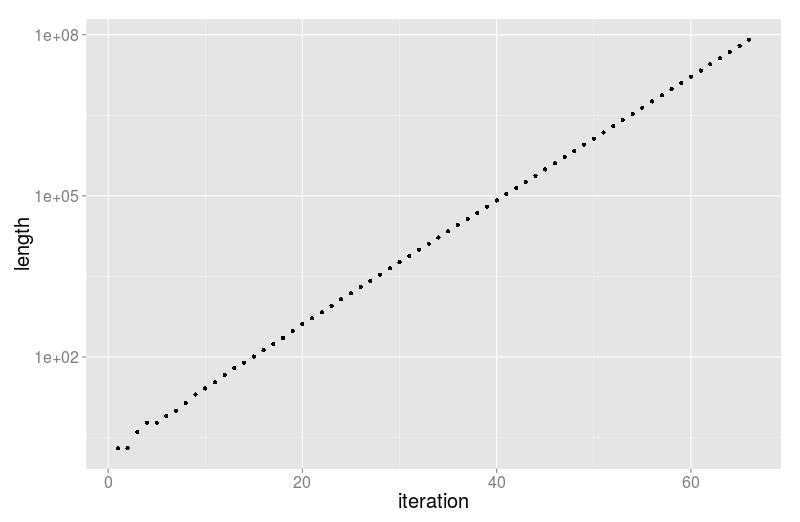
Men… Gad vide om der er nogen orden i eller regler for hvordan det stiger? Vi kan jo starte med de sædvanlige tricks — prøve at gøre akserne logaritmiske, fx, og her ville det jo være oplagt at starte med y-aksen, og så får vi:
Woha! det var da pludselig en utroligt pæn ret linie, hvis man lige ser bort fra det det der fnidder nede i bunden, og vi kan altså konkludere at vi har med en form for eksponentiel vækst at gøre — altså at længden vokser med en konstant faktor per trin, ligesom når man får renter af sine penge (Ja, jeg er så gammel at jeg kan huske positive indlånsrenter!).
Lad os prøve at finde ud af hvilken…
Hvis vi prøver at lægge en ret linie på, så får vi at den har formlen \[ y=0.2680950 \cdot \ln(x) + 0.5731954\] svarende til at \[ \text{length}=1.77\cdot {1.307}^\text{(iteration)}\] og at \(R^2 = 0.9998\).
Hvis vi prøver at fjerne de nederste 10 punkter, bare for at se om det gør nogen forskel at disse irregulære størrelser er med, så får vi næsten det samme udtryk, men værdierne ændrer sig en anelse og overensstemmelsen med en ret linie bliver lidt bedre.
Fjerner vi 10 punkter mere sker det samme igen, bare i lidt mindre grad, og tilsyneladende konvergerer modellen, men det har jeg ikke punkter nok til at vise4 - men det er der en anden der har gjort, nemlig ingen andre end John Conway - ham med “Game of life”5.
Min model, baseret på de sidste 46 punkter er \[ \text{length}=2.03\cdot {1.3038}^\text{(iteration)}\] og Conways konstant er 1.303577269… De 2.03 lader til at være et artefakt — jeg har muligvis lavet en indexeringsfejl et sted, eller nosset i mine startbetingelser, så den har talt fra linie 2… lad mig lige se… jeps - det har jeg. Men det ændrer ikke rigtig noget, så det vil jeg lade være en øvelse for den ivrige l[æø]ser.
Jeg er altså kommet “ret tæt på”6 om end det er en numerisk løsning klyttet sammen og analyseret på en aften.
Konklusionen er altså at længden af talrækken vokser med ca. 30% per iteration. Det er jo en helt fin forrentning, må man sige, og det forklarer jo så glimrende hvorfor den pludselig springer i luften og bliver helt ustyrlig, efter at have startet stille og roligt.
Nå, men… Det var vel hvad der var at sige om dén sag, ud over at der også findes en lille video om det.
Nåja, og selvfølgelig må I få koden til at generere sekvenser med, selvom jeg overgav mig og endte med at bruge den elegante funktionelle version herfra i stedet.
Kod nu forsigtigt, derude!
\Worm
Hvad skal vi lave i morgen aften, Brain?
-
Sikkert under en forelæsning om noget ganske andet — men i det mindste sov jeg da ikke SÅ længe. ↩
-
Jo, det er jeg OGSÅ — det er ifølge min gamle lektor et ønskværdigt træk i en studerende — så gør man tingene rigtigt første gang, fordi man ikke gider lave dem om… ↩
-
Tallet fra iteration 25 er i øvrigt: 1321132132211331121321231231121113112221121321133112132112312321123113112221 12111312211311123113322112132113212231121113112221121321132132211231232112311321 32211231131122211311123113322112111312211312111322111213122112311311123112112322 21121321132132211331121321231231121113121113122122311311222113111231133221121113 12211312111322111213122112311311123112112322211211131221131211132221232112111312 11121311121321123113213221121113122123211211131221222112112322211213211321322113 31121321231231121113112221121321132132211322132113213221123113112221133112132123 22211211131221131211221321123113213221121113122113121132211332113221122112133221 12311311222113111231133211121312211231131112311211133112111312211213211312111322 21123113112211121312211231131122211211133112111311222112111312211312111322211213 21132132212321121113121112133221123113112221131112212211131221121321131211132221 12311311222113111231133221121113311211131122211211131221131112311332211211131221 13121113222123211211131211121332211213211321322113311213212312311211131122211213 21132122311211131122211211131221131211322113322112111312211322132113213221123113 112221131112311311121321122112132231121113122113322113111221131221 — bare hvis du skulle være interesseret :-) ↩
-
Grunden til at jeg i første omgang kun har 66 iterationer med er at min pc løber tør for hukommelse når den når dertil… ↩
-
Der i øvrigt også er en sjov lille øvelse til programmeringsmusklerne for slangetæmmere på mellemniveau. ↩
-
Som ingeniør vil jeg sige “Tæt nok på til alle praktiske forhold”, ligesom i den gamle vittighed om matematikeren, fysikeren og ingeniøren… ↩