Peter Sommers halveringstid
Som Randall Munroe meget skarpt observerer er det utroligt fedt, men kan være lidt distraherende at være tilstrækkeligt nørdet — man finder mønstre og skønhed overalt1.
I går kostede det fx et par timer af min i forvejen sparsomme nattesøvn at jeg opdagede at man på DRs hjemmeside kan se hvor mange gange et bestemt nummer spilles over tid, og efter at have klikket lidt rundt så det ud som om man kunne klassificere forskellige numre efter spillemønster, men det var lidt uoverskueligt, så jeg bed mig fast i at visse numre og kunstnere havde nogle profiler der i mistænkelig grad lignede førsteordens reaktioner, som fx radioaktivt henfald.
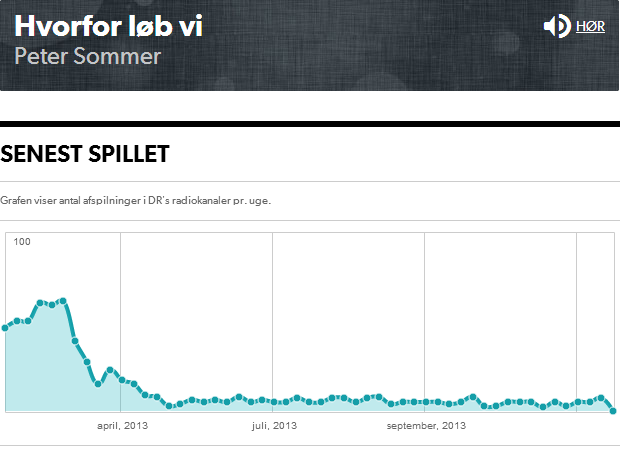
Lidt mere roden rundt fandt et egnet datasæt i Peter Sommers “Hvorfor løb vi”, men da den jo kun viser det sidste år, så er her et screendump til eftertiden:
Lidt mere roden rundt i sovsen fandt at de har lavet grafen ret smart og dynamisk, og at kildedata genereres automagisk og er tilgængelige hvis man kaster en besværgelse over URLen (+= “/GetWeeklyPlays”) og hiver en passende javascriptvariabel ud.2
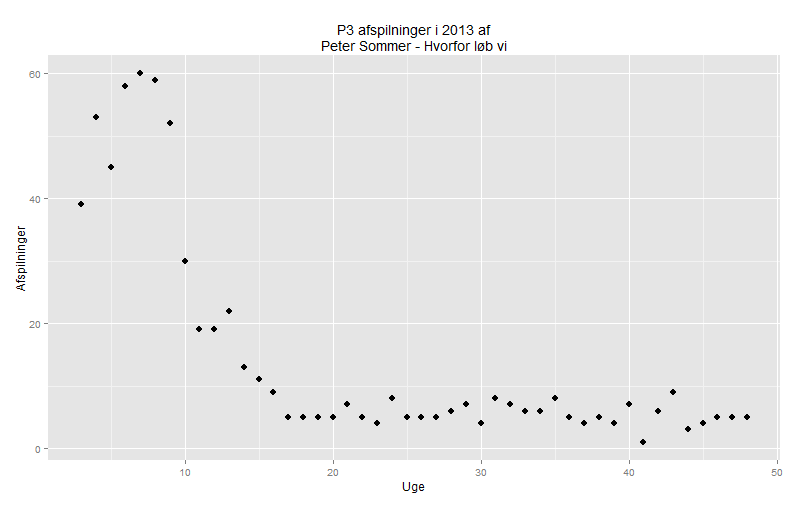
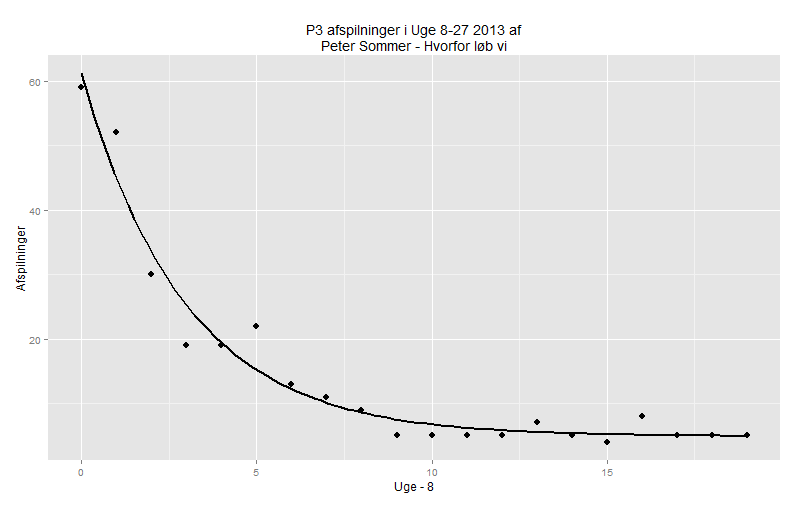
Et par ninjatricks senere havde jeg rådata importeret i R, og kunne genskabe plottet:
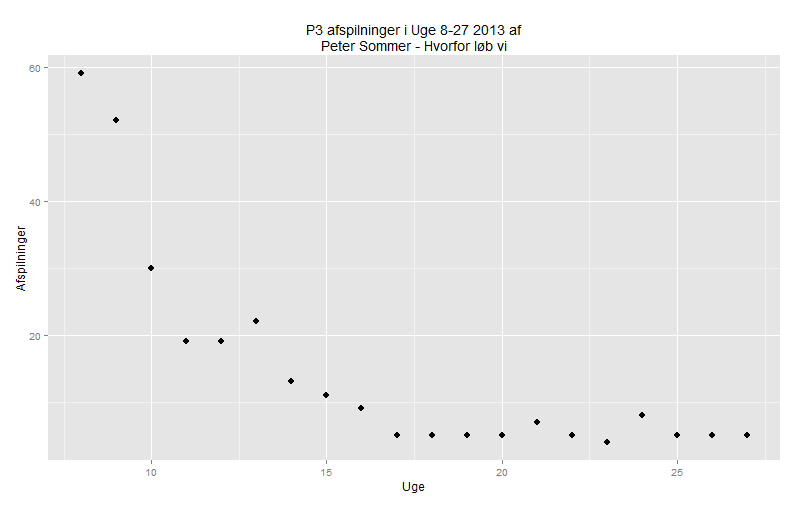
Men hele pointen var jo at se på henfaldsfunktionen, så hvis vi lige beskærer datasættet lidt, fra “toppen af poppen” og til det har nået et stabilt niveau, så får vi følgende:
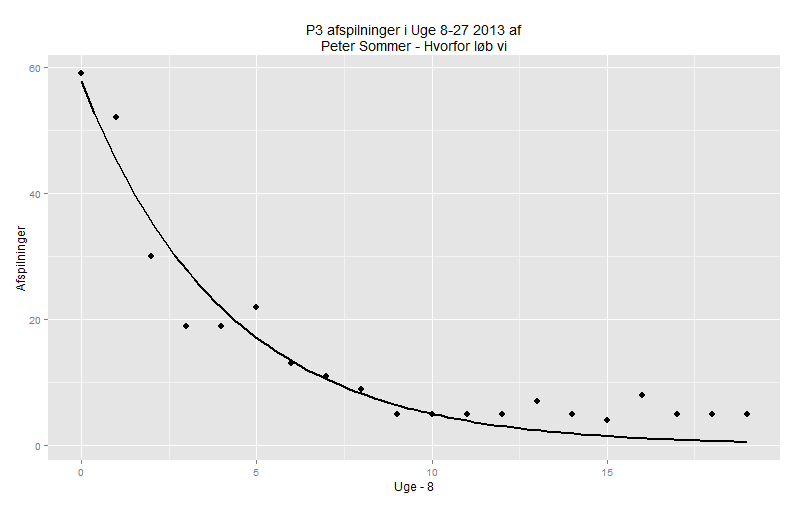
Nu begynder det jo at smage af bladguld på carporten! Det kunne såmænd sagtens være et datasæt fra et forsøg med eksempelvis halveringstid, så lad os forsøge at fitte en model. Her springer jeg let og elefant hen over de sexede detaljer3 og konstaterer at R siger til mig at funktionen \[\text{Afspilninger}=57.74715\cdot e^{-0.24315\cdot\text{Uge}}\] Er det bedste match den kan lave.
Hvis vi lige inspicerer dette visuelt, ser det heller ikke HELT skeløjet ud:
Bemærk at jeg har trukket 8 fra ugenumrene “af tekniske årsager”4 — det er de samme data som ovenfor.
Det ser jo umiddelbart ret pænt ud, men det er akkurat som om funktionen går mod nul (som forventet) og antallet af afspilninger ligger på et konstant niveau, forskelligt fra nul — lad os prøve at indføre en konstant forskydning i antallet og se hvad det så giver…
Jo, minsandten, om ikke det bliver pænere:
Modellen konvergerer hurtigere og residualerne er mindre og alle parametre er stadig signifikant forskellige fra nul, så modellen ser nu således ud: \[\text{Afspilninger}=56.27121\cdot e^{-0.33846\cdot\text{Uge}}+ 4.86232\]
Hvad betyder disse tal så i praksis?
- Da Peter Sommers “Hvorfor løb vi” blev spillet mest på P3 (Uge 8, 2013) blev den i følge modellen spillet 61 gange om ugen - ifølge data 59 gange om ugen. Det er godkendt.
- Nummerets halveringstid er \(t_½=\frac{\ln(2)}{0.33846} \approx 2 \text{ uger}\)
- “Baggrundsstrålingen” udgør ca. 5 afspilninger om ugen, hvilket ifølge ovennævnte musiktracker stadig ser ud til at være gældende.
Det er altså i nogle tilfælde muligt at modellere et nummers popularitet, målt som “antal afspininger på P3” som en simpel førsteordensproces.
Der kan man bare se. Det kunne være sjovt at se om man kunne bruge det til at forudsige hvornår et nummer ryger ud af hitlisterne…og hvor tidligt i forløbet man har signifikante resultater… hmmm… 5
\Worm — fitnisse
-
Også nogle gange hvor de i virkeligheden ikke er — mønstrene i hvert fald… Men det er jo det man har statistik til at afgøre. Vidunderne og skønheden er der alligevel. ↩
-
“Var det ikke hurtigere at skrive tallene du ville have af i hånden?” Spørger du jo nok nu… Jo, det var det helt sikkert — men det er jo ikke sjovt! Det er vigtigt at skille ting ad (mens de virker) — bare man samler dem igen. (Jfr. nummerets indhold) ↩
-
Som man naturligvis kan få tilsendt i en umærket brun konvolut eller email, hvis man måtte have den slags lyster. ↩
-
Det var sent, og jeg gad ikke implementere kompensationen i alle udtrykkene der fulgte. ↩
-
Selvfølgelig er der masser af tilfælde hvor det ikke er gældende, og populariteten enten er stabil eller med komplekse udsving, der muligvis er en sum af flere (forskudte) funktioner, men som von Neumann observerede: “Med 4 parametre kan jeg fitte en elefant. Med 5 kan jeg få den til at vifte med snablen”. ↩