Hvor langt væk er horisonten?
Horisonten er en sjov størrelse — den kan virke tæt på eller langt væk, og uanset hvor hurtigt man bevæger sig, så når man aldrig derhen. Man når måske det sted hvor den var FØR, da man stod et andet sted, men ganske som Tantalus’ æbletræ er den altid udenfor rækkevidde, og det er formodentlig derfor den er så stærkt et symbol — man kan tale om at få udvidet sin horisont, skimte noget i horisonten, eller at noget kan forsvinde “ud over” horisonten (verdens kant / ende, hvis vi går nogle hundrede år tilbage) — både bogstaveligt og symbolsk.
Man kan sige at eftersom man aldrig kan nå den, er det vel ligegyldigt hvor langt den er væk, men det er jo stadig interessant at vide hvad der er den største afstand man kan se fjenden på…
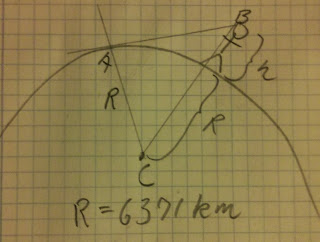
Det er faktisk ikke så besværligt at beregne, når man først lige har fået ideen. Men sådan er det jo med det meste.1 Hvis vi ser på en person med højden \(h\) der står på jorden, som har radius \(R=6371km\)2 så kan vi tegne en trekant med følgende hjørner:
Horisonten — der hvor observatørens sigtelinie er tangent til jordens krumning. Dette punkt kalder vi \(A\). Observatørens øjne — dette punkt kalder vi \(B\). Jordens centrum, \(C\).
Jeg skal være helt ærlig og indrømme at jeg er for doven til at tegne det pænt, men det er cirka sådan noget her vi får:
Idet \(\angle A=90^\circ\) — det er jo en tangent der skærer en radius — kan vi anvende Pythagoras, og få \(|AB|^2 + |AC|^2 = |BC|^2 \), som med lidt fingergymnastik bliver til:
\[\begin{align} |AB|^2 &= |BC|^2 - |AC|^2 \\ |AB| &= \sqrt{|BC|^2 - |AC|^2} \\ |AB| &= \sqrt{(R+h)^2 - R^2} \\ |AB| &= \sqrt{R^2 + h^2 + 2Rh -R^2} \\ |AB| &= \sqrt{h(h+2R)} \end{align}\]Her skal vi jo så huske ikke at blande enhederne — enten skal vi måle folks højde i km (kun tilnærmelsesvist SI-legitimt og upraktisk), eller vi skal måle alle vores afstande i meter, og det giver ikke noget pænt som man kan bruge som tommelfingerregel, uanset hvilken model man anvender, så lad os se om ikke vi kan lave en tilnærmelse eller to og ende med en anvendelig bastardformel.
Men lad os først se hvad vi får, hvis man tager en almindelig øjenhøjde — lad os bare sige 1,75m: \[ |AB| = \sqrt{1,75 \cdot 10^{-3}km \cdot (1,75 \cdot 10^{-3}km + 2 \cdot 6371km)}=4,7km\] Det er tættere på end man umiddelbart ville tro, men passer faktisk fint.
Vi kan nu observere at så længe man er forholdsvist tæt på jorden (lad os bare sige under 1km), så er leddet \( (h+2R) \approx 2R \) og vi kan forsimple formlen til \(|AB| = \sqrt{h \cdot 2R} =\sqrt{h \cdot 12742km}\) og stadig få 4,7 km i ovenstående tilfælde.\
Hvis vi gerne vil regne h i meter, skal vi lige have en faktor mere ind: \(|AB| = \sqrt{h \cdot 10^{-3} \frac{m}{km} \cdot 12742km} \) og da det er et produkt vi har under kvadratroden kan vi flytte alle konstanterne udenfor ved at tage kvadratroden af dem, og få: \(|AB| =3,57 \cdot \sqrt{h}\).3
Altså er afstanden til horisonten, målt i km, for små højder, (h), målt i meter, lig \(3,57 \cdot \sqrt{h}\), og med førnævnte eksempel får vi stadig 4,7 km. Står man på 10 etage og regner med 3m per etage kan man altså se 19,6 km, hvilket jo heller ikke lyder helt skeløjet.
Naturligvis er jeg nødt til at komme med en kommentarer og et forbehold:
- Nej, det er ikke en pæn formel i nogen klassisk forstand, men jeres mobiltelefoner kan jo regne, og på denne må slipper man for at stå og lave Pythagoras i hovedet hver gang.
- Man antager at jorden er perfekt sfærisk, og der er således heller ikke nogle forbehold for lokale geografiske features - på en god dag kan man eksempelvis stå på taget af mine forældres hus og se 30-40 km ud i fædrelandet, og det er ikke fordi de bor i et højhus, men fordi huset ligger på det næsthøjeste punkt i området.
\Worm
-
Måske undtaget kvantemekanik, der jo har den egenskab at hvis man tror man har forstået det, har man sandsynligvis ikke fattet en brik. ↩
-
Ja, jeg ved godt den ikke er en perfekt kugle, men lidt excentricitet er jo en god ting. ↩
-
Ja, jeg sjofler med enhederne. Det må blive en øvelse for den vågne l[æø]ser at udlede dem korrekt ↩